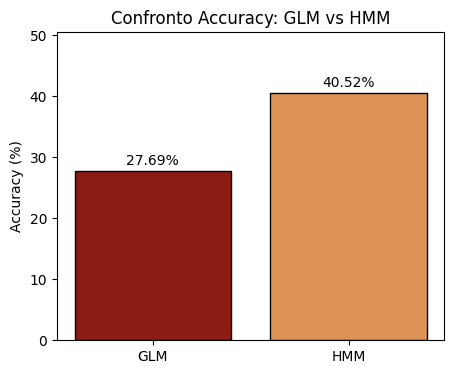Bayesian HMM GLM

Poisson HMM with Covariate-Dependent Emissions

Hidden Markov Model with Poisson emissions. Priors and covariates on initial probabilities and transition matrix. On emission is set up a GLM.

Import and clean data

Import functions and data into the notebook. The data is located in the data folder, while the functions are in the python folder. To enhance the readability of the notebook and reduce code redundancy, certain functions are organized into python files and imported as needed.

from pyprojroot import here
import sys

python_dir = str(here("python"))
if python_dir not in sys.path:
    sys.path.insert(0, python_dir)

%load_ext autoreload
%autoreload 2

The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

# data manipulation
import pandas as pd
import numpy as np
import polars as pl
import torch

# models
from hmmlearn import hmm
from pyprojroot import here
import pyro
import pyro.distributions as dist
import pyro.distributions.constraints as constraints
from pyro.infer import SVI, TraceEnum_ELBO, config_enumerate
from pyro.optim import Adam
from scipy.stats import poisson

# data visualization
import matplotlib.pyplot as plt
from matplotlib import font_manager
import seaborn as sns
# plot settings
from matplotlib import font_manager as fm
from cycler import cycler
# Custom color cycle for plots
plt.rcParams["axes.prop_cycle"] = cycler(color=["#8c1c13ff", "#86ba90ff", "#54403bff"])

# --- Global transparency settings ---
plt.rcParams['figure.facecolor'] = 'none'     # no background color for the figure
plt.rcParams['axes.facecolor'] = 'none'       # no background color for axes
plt.rcParams['savefig.facecolor'] = 'none'    # save figures without background
plt.rcParams['savefig.transparent'] = True    # enable transparency in saved figures

# Custom font
fm.fontManager.addfont(here("python/Figtree-Regular.ttf"))

# Custom state colors
state_cols = ["#8c1c13ff", "#86ba90ff", "#54403bff"]


data = pd.read_csv(here("data/recent_donations.csv"))
data

	unique_number	class_year	birth_year	first_donation_year	gender	y_2009	y_2010	y_2011	y_2012	y_2013	y_2014	y_2015	y_2016	y_2018	y_2019	y_2017	y_2020	y_2021	y_2022	y_2023
0	26308560	(1960,1970]	1965	1985	M	0	0	0	0	0	0	0	0	0	0	0	1	1	3	1
1	26309283	(1960,1970]	1966	2002	M	2	1	2	2	1	1	3	3	4	1	3	3	3	3	4
2	26317365	(1960,1970]	1961	1984	M	4	2	3	3	3	4	3	3	2	3	3	2	0	1	0
3	26318451	(1960,1970]	1967	1989	M	0	3	3	4	4	4	2	3	3	1	2	3	1	0	0
4	26319465	(1960,1970]	1964	1994	F	1	2	2	1	2	1	1	0	0	2	1	1	1	1	1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
9231	27220599	(1970,1980]	1980	2022	M	0	0	0	0	0	0	0	0	0	0	0	0	0	2	0
9232	27220806	(2000,2010]	2002	2022	M	0	0	0	0	0	0	0	0	0	0	0	0	0	2	3
9233	27221247	(1990,2000]	2000	2022	F	0	0	0	0	0	0	0	0	0	0	0	0	0	2	0
9234	27221274	(1960,1970]	1966	2022	F	0	0	0	0	0	0	0	0	0	0	0	0	0	2	3
9235	27221775	(2000,2010]	2004	2022	M	0	0	0	0	0	0	0	0	0	0	0	0	0	2	1

9236 rows × 20 columns

The data is pre-processed via Polars’s library and transformed into torch elements.

# from pandas to polars
df = pl.from_pandas(data)  # or: df = pl.read_csv("file.csv")

# collect donation numbers along years
year_cols = sorted([c for c in df.columns if c.startswith("y_")])
T = len(year_cols)
obs = (
    df.select(year_cols)
      .fill_null(0)
      .to_numpy()
      .astype(int)  # (N,T)
)

# prepare fixed covariates for pi
df = df.with_columns([
    (pl.col("gender") == "F").cast(pl.Int8).alias("gender_code"),
    ((pl.col("birth_year") - pl.col("birth_year").mean()) /
     pl.col("birth_year").std()).alias("birth_year_norm")
])

birth_year_mean = df["birth_year"].to_numpy().mean()
birth_year_std = df["birth_year"].to_numpy().std()
birth_year_norm = df["birth_year_norm"].to_numpy()  # (N,)
gender_code     = df["gender_code"].to_numpy()      # (N,)
intercept = np.ones_like(birth_year_norm)

cov_init = np.stack([intercept, birth_year_norm, gender_code], axis=1)  # (N,2)

# dynamic base: ages (N,T) and covid dummy (N,T)
years_num  = np.array([int(c[2:]) for c in year_cols])  # e.g. [2009, …, 2023]
ages       = years_num[None, :] - df["birth_year"].to_numpy()[:, None]  # (N,T)
ages_squared = ages ** 2

covid_mask  = np.isin(years_num, [2020, 2021, 2022]).astype(float)  # (T,)
covid_years = np.tile(covid_mask, (df.height, 1))                   # (N,T)

# age bins over the FULL df (N,T) -> one-hot (N,T,7)
# bins: [0,25), [25,35), [35,45), [45,55), [55,65), [65,75), [75,120]
age_bins = np.array([0, 25, 35, 45, 55, 60, 65, 85])
ages_binned = np.digitize(ages, age_bins, right=False)   # 1..7
n_agebins = len(age_bins) - 1
ages_binned = np.clip(ages_binned, 1, n_agebins)

ages_onehot = np.eye(n_agebins)[ages_binned - 1][:, :, 1:] # drop the baseline 18-24

intercept_tile = np.ones((ages_onehot.shape[0], ages_onehot.shape[1], 1))  

cov_tran = np.concatenate([
    intercept_tile,
    ages_onehot,                       # (N,T,6)
    covid_years[:, :, None]            # (N,T,1) -> expand with none
], axis=2)

# emission covariates (N,T,9): gender + 7 age-bin dummies + covid
gender_code_tile = np.repeat(gender_code[:, None], T, axis=1)       # (N,T)
cov_emission = np.concatenate([
    intercept_tile,
    gender_code_tile[:, :, None],     # (N,T,1)
    ages_onehot,                      # (N,T,7)
    # ages_squared[:, :, None],
    # ages[:, :, None],
    covid_years[:, :, None],          # (N,T,1)
], axis=2)                            # (N,T,9)

# to torch
obs_torch       = torch.tensor(obs,          dtype=torch.long)   # (N,T)
cov_init_torch  = torch.tensor(cov_init,     dtype=torch.float)  # (N,2)
cov_tran_torch  = torch.tensor(cov_tran,     dtype=torch.float)  # (N,T,8)
cov_emiss_torch = torch.tensor(cov_emission, dtype=torch.float)  # (N,T,9)

print("obs        :", obs_torch.shape)
print("pi covs    :", cov_init_torch.shape)
print("A covs     :", cov_tran_torch.shape)
print("emission   :", cov_emiss_torch.shape)

obs        : torch.Size([9236, 15])
pi covs    : torch.Size([9236, 3])
A covs     : torch.Size([9236, 15, 8])
emission   : torch.Size([9236, 15, 9])

We are planning to create two models:

• Development Model: This model will be used for development purposes, where we will split the observations into training and testing sets. We will evaluate the model’s bias and variance to ensure its reliability and performance.

• Production Model: This model will be integrated into the dashboard, with the primary goal of achieving the best possible predictions. In this case, more data will enhance the model’s predictive power and accuracy. So, we will use the full dataset to train it.

# stratified split 90/10 by gender × age-bin (age at t=0)
N, T = obs_torch.shape
age0 = ages[:, 0]                                          # (N,)
age0_bin = np.digitize(age0, age_bins, right=False)        # 1..7
age0_bin = np.clip(age0_bin, 1, n_agebins)
labels = np.array([f"{int(g)}-{int(b)}" for g, b in zip(gender_code, age0_bin)])

rng = np.random.default_rng(42)
indices = np.arange(N)
test_idx = []
for lab in np.unique(labels):
    idx_lab = indices[labels == lab]
    if idx_lab.size == 0:
        continue
    n_test = max(1, int(np.ceil(0.10 * idx_lab.size)))
    pick = rng.choice(idx_lab, size=n_test, replace=False)
    test_idx.append(pick)

test_idx = np.sort(np.concatenate(test_idx))
train_idx = np.setdiff1d(indices, test_idx)

# subset train and test
obs_train = obs_torch[train_idx]
xpi_train = cov_init_torch[train_idx]
xA_train  = cov_tran_torch[train_idx]
xem_train = cov_emiss_torch[train_idx]  # (N_train, T, 9)

obs_test = obs_torch[test_idx]
xpi_test = cov_init_torch[test_idx]
xA_test  = cov_tran_torch[test_idx]
xem_test  = cov_emiss_torch[test_idx]   # (N_test,  T, 9)

print(f"N train = {obs_train.shape[0]}, N test = {obs_test.shape[0]}")
print("emission (train):", xem_train.shape)
print("emission (test) :", xem_test.shape)

N train = 8308, N test = 928
emission (train): torch.Size([8308, 15, 9])
emission (test) : torch.Size([928, 15, 9])

Covariates names, useful for labeling the plots

import hmm_glm_plots as hmm_pl

# age_bins = np.array([0, 25, 35, 45, 55, 65, 75, 120])
age_years_levels = ["18-24","25-34","35-44","45-54","55-59","60-64", "+65"] # TODO: #2 improve age bins  
ref_age_level = "18-24"

cov_names_pi = [
    "intercept",
    "birth_year_norm",
    "gender_code"
]


age_fac_cols = hmm_pl.expand_factor_names("age_years", age_years_levels, ref_level=ref_age_level)
cov_names_A = ["intercept"] + age_fac_cols + ["covid_years"]
# cov_names_A = ["intercept"] + ["covid_years"]

em_age_fac_cols = hmm_pl.expand_factor_names("age_years", age_years_levels, ref_level=ref_age_level)
# cov_names_em = ["intercept", "gender"] +  ["covid_years"]
# cov_names_em = ["intercept", "gender", "ages_squared" + "ages" + "covid_years"]
cov_names_em = ["intercept", "gender"] + em_age_fac_cols + ["covid_years"]

Model

Let \(x^\pi_n \in \mathbb{R}^2\) encode (birth_year_norm, gender_code), \(x^A_{n,t} \in \mathbb{R}^8\) encode transition covariates (seven age-bin dummies and a covid indicator), and \(x^{em}_{n,t} \in \mathbb{R}^9\) encode emission covariates (gender, seven age-bin dummies, covid).

• Hidden state \(z_{n,t} \in \{0,1,2\}\)
• Observed count \(y_{n,t} \in \mathbb{N}\)

Priors Asymmetric priors are set up to ensure divisibility from on state to other.

• \(\pi_{\text{base}} \sim \mathrm{Dirichlet}(\boldsymbol{\alpha}_\pi)\)

• \(A_{\text{base}}[k,\cdot] \sim \mathrm{Dirichlet}(\boldsymbol{\alpha}_{A_k})\)

Slope parameters to learn

• \(W_\pi \in \mathbb{R}^{K\times 2}\)

• \(W_A \in \mathbb{R}^{K\times K \times 8}\)

• \(\beta_{em} \in \mathbb{R}^{K \times (1+9)}\) (intercept plus 9 slopes for emission GLMs)

Initial-state distribution \[ \Pr(z_{n,0}=k \mid x^\pi_n) = \mathrm{softmax}_k \big( \log \pi_{\text{base},k} + W_{\pi,k} \cdot x^\pi_n \big) \]

Transition distribution \[ \Pr(z_{n,t}=j \mid z_{n,t-1}=k, \ x^A_{n,t}) = \mathrm{softmax}_j \big( \log A_{\text{base},kj} + W_{A,kj} \cdot x^A_{n,t} \big) \]

Emission (State-specific Poisson GLM with age bins) \[ y_{n,t} \mid z_{n,t}=k \sim \mathrm{Poisson}\Big( \exp\Big( X^{em}_{n,t} \mathbf{\beta_{em,k}} \Big) \Big) \]

Variational guide - Point-mass for \(\pi_{\text{base}}\) and \(A_{\text{base}}\) (Delta). - All \(W_\pi\), \(W_A\), \(\beta_{em}\) are deterministic Pyro params.

Training - Loss: TraceEnum_ELBO(max_plate_nesting=1) - Optimizer: Adam(lr = 2e-2) the value is set up manually to get the optimum ELBO with a fixed iterations

K      = 3      # Number of latent states
C_pi   = cov_init.shape[1]      # Initial-state covariates (birth_year_norm, gender_code)
C_A    = cov_tran.shape[2]      # Transition covariates (ages_norm, covid_years)
C_em   = cov_emission.shape[2]      # Emission covariates (gender, 7 age dummies, covid)

# alpha_A  = torch.tensor([
#     [6.,1.,1.],
#     [1.,6.,1.],
#     [1.,1.,6.]
# ])
# alpha_pi = torch.ones(K)

# Asymmetric Dirichlet prior
alpha_pi = torch.tensor([5., 2., 1.])
alpha_A  = torch.ones((K, K))


@config_enumerate
def model(obs, x_pi, x_A, x_em):
    N, T = obs.shape

    # 1) Priors/parameters for initial and transition distribution
    pi_base = pyro.sample("pi_base", dist.Dirichlet(alpha_pi))          # [K]
    A_base  = pyro.sample("A_base",  dist.Dirichlet(alpha_A).to_event(1)) # [K, K]
    log_pi_base = pi_base.log()
    log_A_base  = A_base.log()

    # 2) Slope coefficients for initial and transition covariates (learned)
    W_pi = pyro.param("W_pi", torch.zeros(K, C_pi))                  # [K, C_pi]
    W_A  = pyro.param("W_A", torch.zeros(K, K, C_A))                 # [K, K, C_A]

    # 3) State-specific GLM emission coefficients (learned)
    beta_em = pyro.param("beta_em", torch.zeros(K, C_em))        # [K, C_em+1] (intercept + 9 dummies)

    with pyro.plate("seqs", N):
        # Initial hidden state probabilities: depend on x_pi via W_pi
        logits0 = log_pi_base + (x_pi @ W_pi.T)                      # [N, K]
        z_prev = pyro.sample("z_0",
                             dist.Categorical(logits=logits0),
                             infer={"enumerate": "parallel"})

        # Emission at t=0: state-specific GLM on covariates x_em[:, 0, :]
        log_mu0 = (x_em[:, 0, :] * beta_em[z_prev, :]).sum(-1)
        pyro.sample("y_0", dist.Poisson(log_mu0.exp()), obs=obs[:, 0])

        # For t = 1 ... T-1, update state and emit
        for t in range(1, T):
            x_t = x_A[:, t, :]                                      # [N, C_A]
            logitsT = (log_A_base[z_prev] + (W_A[z_prev] * x_t[:, None, :]).sum(-1))     # [N, K]
            z_t = pyro.sample(f"z_{t}",
                             dist.Categorical(logits=logitsT),
                             infer={"enumerate": "parallel"})

            # Emission: state-specific GLM at time t
            log_mu_t = (x_em[:, t, :] * beta_em[z_t, :]).sum(-1)
            pyro.sample(f"y_{t}", dist.Poisson(log_mu_t.exp()), obs=obs[:, t])
            z_prev = z_t

#  GUIDE: Point-mass for pi_base and A_base, params for all slopes
def guide(obs, x_pi, x_A, x_em):
    pi_q = pyro.param(
        "pi_base_map",
        # torch.ones(K),
        alpha_pi,
        constraint=dist.constraints.simplex
    )

    # Each row: simplex for state-to-state transitions
    A_init = torch.eye(K) * (K - 1.) + 1.
    A_init = A_init / A_init.sum(-1, keepdim=True)
    A_q = pyro.param(
        "A_base_map",
        A_init,
        constraint=dist.constraints.simplex
    )

    pyro.sample("pi_base", dist.Delta(pi_q).to_event(1))
    pyro.sample("A_base",  dist.Delta(A_q).to_event(2))

#  TRAINING: it was run only first time and the saved into models folder
# pyro.clear_param_store()
# svi = SVI(model, guide,
#           Adam({"lr": 2e-2}),
#           loss=TraceEnum_ELBO(max_plate_nesting=1))

# for step in range(4000):
#     loss = svi.step(obs_torch, cov_init_torch, cov_tran_torch, cov_emiss_torch)
#     if step % 200 == 0:
#         print(f"{step:4d}  ELBO = {loss:,.0f}")

# param_path = here("models/hmm_glm_full.pt")
# pyro.get_param_store().save(param_path)
# print(f"ParamStore saved in: {param_path}")

   0  ELBO = 177,712
 200  ELBO = 125,480
 400  ELBO = 124,493
 600  ELBO = 124,251
 800  ELBO = 124,149
1000  ELBO = 124,095
1200  ELBO = 124,062
1400  ELBO = 124,041
1600  ELBO = 124,027
1800  ELBO = 124,016
2000  ELBO = 124,009
2200  ELBO = 124,003
2400  ELBO = 123,998
2600  ELBO = 123,995
2800  ELBO = 123,992
3000  ELBO = 123,989
3200  ELBO = 123,987
3400  ELBO = 123,985
3600  ELBO = 123,984
3800  ELBO = 123,982
ParamStore saved in: d:\GitHub\Blood-Donors\models\hmm_glm_full.pt

To improve the notebook exectution we fit the model only the first time and then loaded

import hmm_glm_model as hmm_glm

# load the parameters
W_pi, W_A, pi_base, A_base, beta_em = hmm_glm.load_hmm_params(here("models/hmm_glm_full.pt"))
# beta_em

# pyro.render_model(model,
#                  model_args=(obs_torch, cov_init_torch, cov_tran_torch, cov_emiss_torch),
#                  render_distributions=True,     # mostra le distribuzioni
#                  render_params=True
#                  ) 

Results

• ELBO steadily decreases from ≈184 k to ≈120 k and then plateaus → optimisation has mostly converged.

• Initial-state distribution \(\pi\) – State 0 dominates (80 %), followed by state 2 (15 %); state 1 is rare (5 %). Most donors start in state 0.

• Transition matrix \(A\)

  • Strong self-persistence: \(P(0 \rightarrow 0)=0.83\), \(P(1 \rightarrow 1)=0.98\), \(P(2 \rightarrow 2)=0.94\).
    
  • Cross-state moves are all < 11 %; once a donor is in a state, they tend to stay there.

• Poisson rates

  • State 0: most of \(\beta\) are negatives. The donation number will be low
  • State 1: the people who belong to state 1 was more propense to donate during the covid, and in th middle ages.
  • State 2: Who donates very frequently and it icreases with the age, but the coid had a bad effect on them

Interpretation: the model has discovered three very stable behavioural profiles -non-donors, heavy donors, and light donors- with rare transitions between them.

def softmax_row(v):
    e = np.exp(v - np.max(v, axis=-1, keepdims=True))
    return e / e.sum(axis=-1, keepdims=True)

x_mean_pi = cov_init_torch.mean(dim=0).detach().cpu().numpy()        # (C_pi,)
x_mean_A  = cov_tran_torch.mean(dim=(0, 1)).detach().cpu().numpy()   # (C_A,)

# 3) Mean initial probs and transitions under average covariates
logits_pi = np.log(pi_base + 1e-30) + W_pi @ x_mean_pi
pi_mean   = softmax_row(logits_pi[None, :]).ravel() # ravel flats the dimensions from (1,N) to (N)

K = pi_mean.shape[0]
A_mean = np.zeros((K, K))
for k in range(K):
    logits_row = np.log(A_base[k] + 1e-30) + (W_A[k] @ x_mean_A)
    A_mean[k] = softmax_row(logits_row[None, :]).ravel()

state_names = [f"State {i}" for i in range(K)]

print("pi mean:", " | ".join(f"{v:.2%}" for v in pi_mean))
print("A mean:\n", np.vectorize(lambda v: f"{v:.2%}")(A_mean))

plots = hmm_pl.plot_hmm_params_with_coeffs(
    transitions=A_mean,
    initial_probs=pi_mean,
    beta_em=beta_em,
    state_names=state_names,
    coeff_names=cov_names_em,
)

pi mean: 81.18% | 6.06% | 12.76%
A mean:
 [['85.29%' '9.57%' '5.14%']
 ['0.80%' '99.20%' '0.00%']
 ['0.00%' '5.03%' '94.97%']]

Diagnostics

Viterbi Algorithm (with covariates and Poisson-GLM emissions)

Goal: For each donor \(n=1..N\), find the MAP latent path \(z_{0:T}^\ast\).

Parameterization (plug-in, posterior means) - Covariate-dependent initial distribution: - Logits for \(\pi\): \(\ell_\pi(x_\pi) = \log \pi_{\text{base}} + W_\pi x_\pi\) - \(\pi(x_\pi) = \text{softmax}(\ell_\pi(x_\pi))\) - Covariate-dependent transition matrix: - Logits for \(A\) at time \(t\): \(\ell_A(x_{A,t})_{k\to j} = \log A_{\text{base}}[k,j] + \langle W_A[k,j,:], x_{A,t} \rangle\) - \(A(x_{A,t})[k,\cdot] = \text{softmax}_j\bigl(\ell_A(x_{A,t})_{k\to j}\bigr)\) - Emissions: - Poisson-GLM per state \(k\): \(\eta_k(t) = \beta_{em,k,0} + x_{\text{em},t}^T \beta_{em,k}\) - \(\lambda_k(t) = \exp\bigl(\eta_k(t)\bigr)\)

Dynamic Programming - Initialization (\(t=0\)):

\[ \delta_0(k)=\log \pi_k(x_\pi)+\log \text{Poisson}(y_0\mid \lambda_k(0)). \]

• Recursion for \(t=1,\dots,T\):

\[ \delta_t(j)=\max_k\bigl[\delta_{t-1}(k)+\log A_{k\to j}(x_{A,t})\bigr]+\log \text{Poisson}(y_t\mid \lambda_j(t)), \]

\[ \psi_t(j)=\arg\max_k\bigl[\delta_{t-1}(k)+\log A_{k\to j}(x_{A,t})\bigr]. \]

• Back-tracking:

\[ z_T^\ast=\arg\max_k \delta_T(k), \]

\[ z_{t-1}^\ast=\psi_t\bigl(z_t^\ast\bigr)\quad\text{for }t=T,\dots,1. \]

import hmm_glm_viterbi as viterbi

paths = viterbi.viterbi_paths_glm(
    obs_torch,
    cov_init_torch,    # (N,C_pi)
    cov_tran_torch,    # (N,T,C_A)
    cov_emiss_torch,    # (N,T,C_em)
    here("models/hmm_glm_full.pt")
)
switch_rate = (paths[:, 1:] != paths[:, :-1]).any(1).float().mean()
print(f"switch rate = {switch_rate:.2%}")

switch rate = 79.86%

State occupancy over time (population view)

Looking the plot, it’s easy to detect a strong movement from state 0 to state 1 during the covid years.

from plotnine import (
    ggplot, aes, geom_line,
    scale_color_manual, scale_x_continuous, scale_y_continuous,
    labs, theme_minimal, theme, element_text
)

# it works for torch and numpy elements
paths_np = paths.detach().cpu().numpy() if hasattr(paths, "detach") else np.asarray(paths)
N, T = paths_np.shape
K = int(paths_np.max()) + 1 if paths_np.size else 1

# Counts per state over time -> (K,T)
counts = np.stack([(paths_np == k).sum(axis=0) for k in range(K)], axis=0)
props = counts / np.maximum(counts.sum(axis=0, keepdims=True), 1)  # avoid div-by-zero

rows = []
for k in range(K):
    for t in range(T):
        rows.append({"t": t, 
        "state": f"state {k}", "share": float(props[k, t])})
df = pd.DataFrame(rows)

(ggplot(df, aes("t", "share", color="state"))
+ geom_line(size=1.1)
+ scale_color_manual(values=state_cols, name="state")
+ scale_x_continuous(breaks=list(range(T)))
+ scale_y_continuous(limits=(0, 1))
+ labs(x="year index", y="population share", title="State occupancy over time")
+ theme_minimal()
+ theme(axis_text_x=element_text(rotation=0)))

Individual trajectories

Pick a few donors and overlay observations + decoded state for an easy interpretation of the model.

years_axis  = np.arange(2009, 2024)
yticks_vals = np.arange(0, 5)

hmm_pl.plot_one_gg(
        idx=3012,
        obs_torch=obs_torch,
        paths=paths,
        years=years_axis,
        state_cols=None,
        y_max=4
    )

hmm_pl.plot_one_gg(
        idx=1002,
        obs_torch=obs_torch,
        paths=paths,
        years=years_axis,
        state_cols=None,
        y_max=4
    )

hmm_pl.plot_W_pi_heat(W_pi, cov_names_pi)
hmm_pl.plot_W_A_heat(W_A, cov_names_A)
hmm_pl.plot_beta_em_heat(beta_em, cov_names_em)

Covariates

# TODO: #3 Bar chart
# age_bins = np.array([18, 26, 36, 46, 56, 61, 66, 200])  # 7 bands => 7 dummies
# age_bins = bins_split

def age_labels_from_bins(edges: np.ndarray) -> list[str]:
    labels = [f"{a}-{b-1}" for a, b in zip(edges[:-2], edges[1:-1])]
    labels.append(f"{edges[-2]}+")
    return labels

age_levels = age_labels_from_bins(age_bins)  # ["18-25", "26-35", ..., "66+"]


if "ages" not in globals() or "covid_years" not in globals():
    # Requires df and year_cols from your earlier prep
    years_num  = np.array([int(c[2:]) for c in year_cols])            # [2009,...]
    ages       = years_num[None, :] - df["birth_year"].to_numpy()[:, None]  # (N,T)
    covid_mask = np.isin(years_num, [2020, 2021, 2022]).astype(float) # (T,)
    covid_years = np.tile(covid_mask, (ages.shape[0], 1))             # (N,T)


L = len(age_levels)                            # 7
ages_bin = np.digitize(ages, age_bins, right=False) - 1  # 0..6
ages_bin = np.clip(ages_bin, 0, L - 1)
ages_onehot = np.eye(L, dtype=float)[ages_bin]           # (N,T,7)
x_A_data = np.concatenate([ages_onehot, covid_years[..., None]], axis=2)  # (N,T,8)

# 4) Names and factor spec
cov_names_A = [f"age_years[{lab}]" for lab in age_levels] + ["covid_years"]
factor_specs_A = {"age_years": {"levels": age_levels, "ref": None}}  # full one-hot

# 5) Load/prepare model params (W_A, log_A0) as NumPy
try:
    import pyro
    W_A = pyro.param("W_A").detach().cpu().numpy()                   # (K,K,8)
    A_base = pyro.param("A_base_map").detach().cpu().numpy()         # (K,K)
except Exception:
    # Assume already defined in the notebook
    pass
log_A0 = np.log(A_base + 1e-30)


#    - Binary plot for covid_years
hmm_pl.plot_trans_vs_cov_orig(
    var="covid_years",
    prev_state=0,
    cov_names_A=cov_names_A,
    x_A_data=x_A_data,
    W_A=W_A,
    log_A0=log_A0,
    grid_orig=np.array([0.0, 1.0])
)

array([[0.79854764, 0.09986471, 0.10158765],
       [0.1726067 , 0.70509713, 0.12229617]])

import hmm_glm_plots as hmm_pl

def build_factor_cols_compat(cov_names, factor_name, levels, ref_level):
    """
    Return:
      - factor_map: dict level -> column index (or None for reference)
      - all_dummy_idx: list of column indices for all non-reference dummies
    Assumes dummy columns are named like: f"{factor_name}[{level}]".
    If ref_level is None, all levels get a dummy column.
    """
    name_to_idx = {n: i for i, n in enumerate(cov_names)}
    factor_map = {}
    all_dummy_idx = []

    for lev in levels:
        col_name = f"{factor_name}[{lev}]"
        if ref_level is not None and lev == ref_level:
            # reference: no column
            factor_map[lev] = None
        else:
            if col_name not in name_to_idx:
                raise ValueError(f"Missing dummy column '{col_name}' in cov_names for factor '{factor_name}'.")
            idx = name_to_idx[col_name]
            factor_map[lev] = idx
            all_dummy_idx.append(idx)

    return factor_map, all_dummy_idx

# Monkey-patch
hmm_pl.build_factor_cols = build_factor_cols_compat

# Re-run your plot call (same as before)
hmm_pl.plot_trans_vs_cov_orig(
    var="age_years",
    prev_state=0,
    cov_names_A=cov_names_A,
    x_A_data=x_A_data,
    W_A=W_A,
    log_A0=log_A0,
    factor_specs_A=factor_specs_A
)

array([[9.06958211e-01, 6.90374701e-02, 2.40043192e-02],
       [6.06506584e-01, 2.20036616e-01, 1.73456800e-01],
       [5.92306200e-01, 2.10618699e-01, 1.97075102e-01],
       [5.80915558e-01, 2.08525475e-01, 2.10558967e-01],
       [4.51344146e-01, 2.16806106e-01, 3.31849748e-01],
       [3.27382742e-01, 3.37706679e-01, 3.34910579e-01],
       [4.65245805e-01, 5.34291611e-01, 4.62584332e-04]])

factor_specs_pi = {}

def levels_from_cov_names(cov_names, factor):
    pref = f"{factor}["
    return [c[c.find("[")+1:-1] for c in cov_names if c.startswith(pref) and c.endswith("]")]
present_levels = levels_from_cov_names(cov_names_em, "age_years")
ref_level = "0-24" if "0-24" not in present_levels else None

age_levels_used = ([ref_level] if ref_level is not None else []) + present_levels

factor_specs_em = {
    "age_years": {
        "levels": age_levels_used,
        "ref": ref_level
    },
    "covid_years": {
        "levels:"
    }
}

# cov_names_A = [f"age_years[{lab}]" for lab in age_levels] + ["covid_years"]

# cov_names_em = ["gender_code"] + [f"age_years[{lab}]" for lab in age_levels] + ["covid_years"]

log_pi0 = np.log(np.clip(pi_base, 1e-30, None))


hmm_pl.plot_pi_vs_cov_orig(
    df=df,
    ages=ages,
    var="birth_year_norm",
    cov_names_pi=cov_names_pi,
    W_pi=W_pi,
    log_pi0=log_pi0,
    x_pi_data=cov_init,
    factor_specs_pi=factor_specs_pi
)

# π_k(x) vs gender_code (binaria)
hmm_pl.plot_pi_vs_cov_orig(
    df=df,
    ages=ages,
    var="gender_code",
    cov_names_pi=cov_names_pi,
    W_pi=W_pi,
    log_pi0=log_pi0,
    x_pi_data=cov_init,
    factor_specs_pi=factor_specs_pi
)

# λ_k(emissione) vs age_years (fattore con 7 livelli)
# print(cov_names_em)

hmm_pl.plot_lambda_em_vs_cov(
    var_em="age_years",
    beta_em=beta_em,
    cov_names_em=cov_names_em,
    x_em_data=cov_emission,
    factor_specs_em=factor_specs_em    # levels=age_levels, ref=None
)

(['0-24', '25-34', '35-44', '45-54', '55-59', '60-64', '+65'],
 array([[1.90369916e-06, 6.62457439e-01, 3.36127927e+00],
        [3.05939642e-07, 6.07614649e-01, 3.37892873e+00],
        [2.02194110e-07, 6.58043756e-01, 3.54476334e+00],
        [1.01597020e-06, 7.00892021e-01, 3.74216380e+00],
        [1.97052504e-05, 7.13487897e-01, 3.97236918e+00],
        [1.11491837e-06, 6.77024531e-01, 4.09345630e+00],
        [1.31005848e-06, 5.96143197e-01, 3.87177964e+00]]))

Train and test

Let’s split the DB into 2 parts, one will be used for the training and the other one for the testing. After the training of the model the test part will be used to get the probabilities about the donor and its donation the next year. Furthermore, we want to analyze the past latent state of the person.

xem_train.shape

torch.Size([8308, 15, 9])

@config_enumerate
def model(obs, x_pi, x_A, x_em):
    N, T = obs.shape

    # 1) Priors/parameters for initial and transition distribution
    pi_base = pyro.sample("pi_base", dist.Dirichlet(alpha_pi))          # [K]
    A_base  = pyro.sample("A_base",  dist.Dirichlet(alpha_A).to_event(1)) # [K, K]
    log_pi_base = pi_base.log()
    log_A_base  = A_base.log()

    # 2) Slope coefficients for initial and transition covariates (learned)
    W_pi = pyro.param("W_pi", torch.zeros(K, C_pi))                  # [K, C_pi]
    W_A  = pyro.param("W_A", torch.zeros(K, K, C_A))                 # [K, K, C_A]

    # 3) State-specific GLM emission coefficients (learned)
    beta_em = pyro.param("beta_em", torch.zeros(K, C_em))        # [K, C_em+1] (intercept + 9 dummies)

    with pyro.plate("seqs", N):
        # Initial hidden state probabilities: depend on x_pi via W_pi
        logits0 = log_pi_base + (x_pi @ W_pi.T)                      # [N, K]
        z_prev = pyro.sample("z_0",
                             dist.Categorical(logits=logits0),
                             infer={"enumerate": "parallel"})

        # Emission at t=0: state-specific GLM on covariates x_em[:, 0, :]
        log_mu0 = (x_em[:, 0, :] * beta_em[z_prev, :]).sum(-1)
        pyro.sample("y_0", dist.Poisson(log_mu0.exp()), obs=obs[:, 0])

        # For t = 1 ... T-1, update state and emit
        for t in range(1, T):
            x_t = x_A[:, t, :]                                      # [N, C_A]
            logitsT = (log_A_base[z_prev] + (W_A[z_prev] * x_t[:, None, :]).sum(-1))     # [N, K]
            z_t = pyro.sample(f"z_{t}",
                             dist.Categorical(logits=logitsT),
                             infer={"enumerate": "parallel"})

            # Emission: state-specific GLM at time t
            log_mu_t = (x_em[:, t, :] * beta_em[z_t, :]).sum(-1)
            pyro.sample(f"y_{t}", dist.Poisson(log_mu_t.exp()), obs=obs[:, t])
            z_prev = z_t

#  GUIDE: Point-mass for pi_base and A_base, params for all slopes
def guide(obs, x_pi, x_A, x_em):
    pi_q = pyro.param(
        "pi_base_map",
        torch.tensor([0.6, 0.3, 0.1]),
        constraint=dist.constraints.simplex
    )

    # Each row: simplex for state-to-state transitions
    A_init = torch.eye(K) * (K - 1.) + 1.
    A_init = A_init / A_init.sum(-1, keepdim=True)
    A_q = pyro.param(
        "A_base_map",
        A_init,
        constraint=dist.constraints.simplex
    )

    pyro.sample("pi_base", dist.Delta(pi_q).to_event(1))
    pyro.sample("A_base",  dist.Delta(A_q).to_event(2))

# pyro.clear_param_store()
# svi = SVI(model, guide, Adam({"lr": 5e-2}), loss=TraceEnum_ELBO(max_plate_nesting=1))

# for step in range(2000):
#     loss = svi.step(obs_train, xpi_train, xA_train, xem_train)
#     if step % 200 == 0:
#         print(f"{step:4d}  ELBO(train) = {loss:,.0f}")

# # # # save the model
# pyro.get_param_store().save(here("models/hmm_glm_train.pt"))
# print("Fitted and saved: rates, W_pi, W_A, pi_base_map, A_base_map")

   0  ELBO(train) = 160,215
 200  ELBO(train) = 112,172
 400  ELBO(train) = 111,974
 600  ELBO(train) = 111,924
 800  ELBO(train) = 111,903
1000  ELBO(train) = 111,892
1200  ELBO(train) = 111,886
1400  ELBO(train) = 111,882
1600  ELBO(train) = 111,879
1800  ELBO(train) = 111,877
Fitted and saved: rates, W_pi, W_A, pi_base_map, A_base_map

Load the model and store the parameters

W_pi, W_A, pi_base, A_base, beta_em = hmm_glm.load_hmm_params(here("models/hmm_glm_train.pt"))
order = hmm_glm._simple_order_by_pi0(pi_base)
pi_base, A_base, W_pi, W_A, beta_em, _ = hmm_glm.reorder_params(order, pi_base, A_base, W_pi, W_A, beta_em)

def log_softmax_logits(logits, dim=-1):
    return logits - torch.logsumexp(logits, dim=dim, keepdim=True)


@torch.no_grad()
def forward_loglik_cov(obs, x_pi, x_A, x_em, model_path="models/hmm_glm_train.pt"):
    device = obs.device

    W_pi, W_A, pi_base, A_base, beta_em = hmm_glm.load_hmm_params(here(model_path))


    W_pi    = torch.as_tensor(W_pi,    device=device, dtype=torch.float32)
    W_A     = torch.as_tensor(W_A,     device=device, dtype=torch.float32)
    pi_base = torch.as_tensor(pi_base, device=device, dtype=torch.float32)
    A_base  = torch.as_tensor(A_base,  device=device, dtype=torch.float32)
    beta_em = torch.as_tensor(beta_em, device=device, dtype=torch.float32)

    N, T = obs.shape
    B  = beta_em
    log_mu = torch.einsum("ntc,kc->ntk", x_em, B)
    emis_log = dist.Poisson(rate=log_mu.exp()).log_prob(obs.unsqueeze(-1))

    log_pi = log_softmax_logits(pi_base.log() + x_pi @ W_pi.T, dim=1)
    log_alpha = log_pi + emis_log[:, 0]

    log_A0 = A_base.log()
    for t in range(1, T):
        x_t = x_A[:, t, :]
        logits = log_A0.unsqueeze(0) + (W_A.unsqueeze(0) * x_t[:, None, None, :]).sum(-1)
        log_A = log_softmax_logits(logits, dim=2)
        log_alpha = torch.logsumexp(log_alpha.unsqueeze(2) + log_A, dim=1) + emis_log[:, t]
    return torch.logsumexp(log_alpha, dim=1)


@torch.no_grad()
def one_step_ahead_metrics(obs, x_pi, x_A, x_em, model_path="models/hmm_glm_train.pt"):
    import numpy as np
    device = obs.device

    W_pi, W_A, pi_base, A_base, beta_em = hmm_glm.load_hmm_params(here(model_path))
    order = hmm_glm._simple_order_by_pi0(pi_base)
    pi_base, A_base, W_pi, W_A, beta_em, _ = hmm_glm.reorder_params(order, pi_base, A_base, W_pi, W_A, beta_em)

    W_pi    = torch.as_tensor(W_pi,    device=device, dtype=torch.float32)
    W_A     = torch.as_tensor(W_A,     device=device, dtype=torch.float32)
    pi_base = torch.as_tensor(pi_base, device=device, dtype=torch.float32)
    A_base  = torch.as_tensor(A_base,  device=device, dtype=torch.float32)
    beta_em = torch.as_tensor(beta_em, device=device, dtype=torch.float32)

    N, T = obs.shape
    K = pi_base.shape[0]
    B  = beta_em
    log_mu = torch.einsum("ntc,kc->ntk", x_em, B)
    emis_log = dist.Poisson(rate=log_mu.exp()).log_prob(obs.unsqueeze(-1))

    log_pi = log_softmax_logits(pi_base.log() + x_pi @ W_pi.T, dim=1)
    log_alpha = torch.empty(N, T, K, device=device)
    log_alpha[:, 0] = log_pi + emis_log[:, 0]
    alpha_norm = (log_alpha[:, 0] - torch.logsumexp(log_alpha[:, 0], dim=1, keepdim=True)).exp()

    preds_mean, preds_pdon, logscore, y_next_all = [], [], [], []
    log_A0 = A_base.log()

    for t in range(0, T - 1):
        x_t1 = x_A[:, t + 1, :]
        logits = log_A0.unsqueeze(0) + (W_A.unsqueeze(0) * x_t1[:, None, None, :]).sum(-1)
        log_A = log_softmax_logits(logits, dim=2)

        P_next = torch.exp(torch.log(alpha_norm + 1e-40).unsqueeze(1) + log_A).sum(dim=2)
        log_mu_t1 = torch.einsum("nc,kc->nk", x_em[:, t + 1, :], B)
        lam_ntk = log_mu_t1.exp()

        Ey  = (P_next * lam_ntk).sum(dim=1)
        P0  = (P_next * torch.exp(-lam_ntk)).sum(dim=1)
        Pdon = 1.0 - P0

        y_next = obs[:, t + 1]
        pmf_k = torch.stack([torch.exp(dist.Poisson(lam_ntk[:, k]).log_prob(y_next)) for k in range(K)], dim=1)
        mix_pmf = (P_next * pmf_k).sum(dim=1).clamp_min(1e-12)
        ls = torch.log(mix_pmf)

        preds_mean.append(Ey.cpu().numpy())
        preds_pdon.append(Pdon.cpu().numpy())
        logscore.append(ls.cpu().numpy())
        y_next_all.append(y_next.cpu().numpy())

        log_alpha[:, t + 1] = torch.logsumexp(log_alpha[:, t].unsqueeze(2) + log_A, dim=1) + emis_log[:, t + 1]
        alpha_norm = (log_alpha[:, t + 1] - torch.logsumexp(log_alpha[:, t + 1], dim=1, keepdim=True)).exp()

    Ey = np.concatenate(preds_mean)
    Pd = np.concatenate(preds_pdon)
    LS = np.concatenate(logscore)
    Y  = np.concatenate(y_next_all)

    mae = np.mean(np.abs(Ey - Y))
    rmse = np.sqrt(np.mean((Ey - Y) ** 2))
    brier = np.mean((Pd - (Y > 0).astype(float)) ** 2)
    nll = -np.mean(LS)
    return {"MAE": mae, "\nRMSE": rmse, "\nBrier(y>0)": brier, "\nNLL": nll}

# TODO #4 move to GPU
# Now we're using CPU, but in the future would be nice to swith to GPU
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

obs_test_d  = obs_test.to(device)
xpi_test_d  = xpi_test.to(device)
xA_test_d   = xA_test.to(device)
xem_test_d  = xem_test.to(device)

ll_test = forward_loglik_cov(obs_test_d, xpi_test_d, xA_test_d, x_em=xem_test_d, model_path="models/hmm_glm_train.pt")
print(f"Test mean log-likelihood per seq: {ll_test.mean().item():.3f}")

metrics = one_step_ahead_metrics(obs_test_d, xpi_test_d, xA_test_d, x_em=xem_test_d, model_path="models/hmm_glm_train.pt")
print("One-step-ahead metrics (test):", metrics)

obs_train_d = obs_train.to(device)
xpi_train_d = xpi_train.to(device)
xA_train_d  = xA_train.to(device)
xem_train_d = xem_train.to(device)

ll_train = forward_loglik_cov(obs_train_d, xpi_train_d, xA_train_d, x_em=xem_train_d, model_path="models/hmm_glm_train.pt")
metrics_tr = one_step_ahead_metrics(obs_train_d, xpi_train_d, xA_train_d, x_em=xem_train_d, model_path="models/hmm_glm_train.pt")
print(f"Train mean log-likelihood per seq: {ll_train.mean().item():.3f}")
print("One-step-ahead metrics (train):", metrics_tr)

Test mean log-likelihood per seq: -13.050
One-step-ahead metrics (test): {'MAE': np.float64(0.5074462074848933), '\nRMSE': np.float64(0.7679371621220419), '\nBrier(y>0)': np.float64(0.17972213163887893), '\nNLL': np.float32(0.8822957)}
Train mean log-likelihood per seq: -13.467
One-step-ahead metrics (train): {'MAE': np.float64(0.5188324047583133), '\nRMSE': np.float64(0.7834984557894435), '\nBrier(y>0)': np.float64(0.17898465628283766), '\nNLL': np.float32(0.91493595)}

def _softmax_row(x):
    x = x - x.max(axis=-1, keepdims=True)
    e = np.exp(x)
    return e / e.sum(axis=-1, keepdims=True)


@torch.no_grad()
def predict_donor(
    birth_year: int,
    gender: str,
    history_years: list,
    history_counts: list,
    next_year: int | None = None,
    max_k: int = 4,
    covid_years=(2020, 2021, 2022),
    model_path="models/hmm_glm_train.pt"
):
    years = np.array(history_years, dtype=int)
    yvals = np.array(history_counts, dtype=int)
    if next_year is None:
        next_year = int(years[-1] + 1)

    W_pi, W_A, pi_base, A_base, beta_em = hmm_glm.load_hmm_params(here(model_path))
    order = hmm_glm._simple_order_by_pi0(pi_base)
    pi_base, A_base, W_pi, W_A, beta_em, inv = hmm_glm.reorder_params(order, pi_base, A_base, W_pi, W_A, beta_em)

    K = int(pi_base.shape[0])

    g_code = 1.0 if gender.upper().startswith("F") else 0.0
    by_norm = (birth_year - birth_year_mean) / birth_year_std

    age_bins = np.array([18, 25, 35, 45, 55, 60, 65, 75])
    ages_arr = years - birth_year
    ages_binned = np.digitize(ages_arr, age_bins, right=False)
    n_agebins = len(age_bins) - 1
    ages_binned = np.clip(ages_binned, 1, n_agebins)
    ages_onehot = np.eye(n_agebins)[ages_binned - 1][:, 1:]
    covid_flag = np.isin(years, covid_years).astype(float)[:, None]

    x_pi_np = np.array([[1.0, by_norm, g_code]], dtype=np.float32)
    intercept = np.ones((len(years), 1), dtype=np.float32)

    x_A_hist = np.concatenate([intercept, ages_onehot.astype(np.float32), covid_flag.astype(np.float32)], axis=1)
    age_next = np.array([next_year - birth_year])
    ages_binned_next = np.digitize(age_next, age_bins, right=False)
    ages_binned_next = np.clip(ages_binned_next, 1, n_agebins)
    ages_onehot_next = np.eye(n_agebins)[ages_binned_next - 1][:, 1:]
    covid_next_flag = np.array([[1.0 if next_year in covid_years else 0.0]], dtype=np.float32)
    x_A_next = np.concatenate([np.ones((1,1), dtype=np.float32), ages_onehot_next.astype(np.float32), covid_next_flag], axis=1)[0]

    gender_col = np.full((len(years), 1), g_code, dtype=np.float32)
    x_em_hist = np.concatenate([intercept, gender_col, ages_onehot.astype(np.float32), covid_flag.astype(np.float32)], axis=1)
    x_em_next = np.concatenate([np.ones((1,1), dtype=np.float32), np.array([[g_code]], dtype=np.float32), ages_onehot_next.astype(np.float32), covid_next_flag], axis=1)[0]

    obs_te  = torch.tensor(yvals[None, :], dtype=torch.long)
    xpi_te  = torch.tensor(x_pi_np, dtype=torch.float32)
    xA_te   = torch.tensor(x_A_hist[None, :, :], dtype=torch.float32)
    xem_te  = torch.tensor(x_em_hist[None, :, :], dtype=torch.float32)

    paths_old = viterbi.viterbi_paths_glm(obs_te, xpi_te, xA_te, xem_te, model_path=here(model_path))
    v_path = inv[paths_old.cpu().numpy()[0]].tolist()

    B = torch.tensor(beta_em, dtype=torch.float32)
    emis_log = dist.Poisson(rate=torch.einsum("ntc,kc->ntk", xem_te, B).exp()).log_prob(obs_te.unsqueeze(-1))

    W_pi_t = torch.tensor(W_pi, dtype=torch.float32)
    log_pi0 = torch.tensor(np.log(pi_base + 1e-30) + (x_pi_np @ W_pi.T), dtype=torch.float32)
    log_pi = log_pi0 - torch.logsumexp(log_pi0, dim=1, keepdim=True)

    K = pi_base.shape[0]
    T_hist = obs_te.size(1)
    log_alpha = torch.empty(1, T_hist, K, dtype=torch.float32)
    log_alpha[:, 0] = log_pi + emis_log[:, 0]

    logA0 = torch.tensor(np.log(A_base + 1e-30), dtype=torch.float32)
    W_A_t = torch.tensor(W_A, dtype=torch.float32)
    for t in range(1, T_hist):
        x_t = xA_te[:, t, :]
        logits = logA0.unsqueeze(0) + (W_A_t.unsqueeze(0) * x_t[:, None, None, :]).sum(-1)
        log_A  = logits - torch.logsumexp(logits, dim=2, keepdim=True)
        log_alpha[:, t] = torch.logsumexp(log_alpha[:, t - 1].unsqueeze(2) + log_A, dim=1) + emis_log[:, t]
    alpha_T = (log_alpha[:, -1] - torch.logsumexp(log_alpha[:, -1], dim=1, keepdim=True)).exp().cpu().numpy()[0]

    logits_next = np.log(A_base + 1e-30) + np.tensordot(W_A, x_A_next, axes=([2], [0]))
    A_next = _softmax_row(logits_next)
    p_next = alpha_T @ A_next

    lam_next = np.exp(beta_em @ x_em_next)
    expected_next = float((p_next * lam_next).sum())
    p0 = float((p_next * np.exp(-lam_next)).sum())
    prob_donate_next = 1.0 - p0

    from scipy.stats import poisson as _po
    pmf0k = np.array([(p_next * _po.pmf(k, lam_next)).sum() for k in range(max_k + 1)], dtype=float)
    tail  = float(max(0.0, 1.0 - pmf0k.sum()))
    pmf_dict = {str(k): float(pmf0k[k]) for k in range(max_k + 1)}
    pmf_dict[f">={max_k+1}"] = tail

    return {
        "years": history_years,
        "counts": history_counts,
        "viterbi_states": v_path,
        "next_year": int(next_year),
        "next_state_probs": p_next.tolist(),
        "expected_next": expected_next,
        "prob_donate_next": prob_donate_next,
        "pmf_next": pmf_dict
    }

# stats = np.load("norm_stats.npz")
# birth_year_mean = float(stats["birth_year_mean"])
# birth_year_std  = float(stats["birth_year_std"])
# ages_mean       = float(stats["ages_mean"])
# ages_std        = float(stats["ages_std"])

birth_year = 1985
gender = "F"
history_years   = list(range(2009, 2024))
history_counts  = [0,1,0,0,1,0,0,1,0,0,1,0,1,0,0]
next_year = 2024

out = predict_donor(
    birth_year=birth_year,
    gender=gender,
    history_years=history_years,
    history_counts=history_counts,
    next_year=next_year,
    max_k=4,
    model_path="models/hmm_glm_train.pt"
)

print("Years:", out["years"])
print("Counts:", out["counts"])
print("Viterbi states:", out["viterbi_states"])
print("Next year:", out["next_year"])
print("Next-state probabilities:", np.round(out["next_state_probs"], 3))
print("Expected next:", round(out["expected_next"], 3))
print("Prob donate next:", round(out["prob_donate_next"], 3))
print("PMF next:", {k: round(v, 4) for k, v in out["pmf_next"].items()})

Years: [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023]
Counts: [0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0]
Viterbi states: [0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
Next year: 2024
Next-state probabilities: [0.108 0.016 0.876]
Expected next: 0.565
Prob donate next: 0.417
PMF next: {'0': 0.5828, '1': 0.2984, '2': 0.0946, '3': 0.0203, '4': 0.0034, '>=5': 0.0005}

i = 991
years_hist = years_num[:-1].tolist()
year_next  = int(years_num[-1])
counts_hist = obs_torch[i, :len(years_hist)].detach().cpu().numpy().tolist()

birth_year_i = int(data["birth_year"][i])
gender_i     = data["gender"][i]

pred = predict_donor(
    birth_year=birth_year_i,
    gender=gender_i,
    history_years=years_hist,
    history_counts=counts_hist,
    next_year=year_next,
    max_k=4,
    model_path="models/hmm_glm_train.pt"
)

T_hist = len(years_hist)
N = obs_torch.shape[0]
paths = np.zeros((N, T_hist), dtype=int)
paths[i, :] = np.asarray(pred["viterbi_states"], dtype=int)

print("Years:", pred["years"])
print("Counts:", pred["counts"])
print("Viterbi states:", pred["viterbi_states"])
print("Next year:", pred["next_year"])
print("Next-state probabilities:", np.round(pred["next_state_probs"], 3))
print("Expected next:", round(pred["expected_next"], 3))
print("Prob donate next:", round(pred["prob_donate_next"], 3))
print("PMF next:", {k: round(v, 4) for k, v in pred["pmf_next"].items()})

y_true_next = int(obs_torch[i, T_hist].detach().cpu().item())
p = hmm_pl.plot_donor_gg(
    idx=2000,
    obs_torch=obs_torch[:, :T_hist],
    paths=paths,
    years=years_hist,
    expected_next=pred["expected_next"],
    y_true_next=y_true_next,
    next_year=year_next,
    y_max=4
)
p

Years: [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022]
Counts: [0, 0, 0, 0, 0, 0, 1, 1, 0, 2, 1, 1, 1, 2]
Viterbi states: [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1]
Next year: 2023
Next-state probabilities: [0.02 0.44 0.54]
Expected next: 0.918
Prob donate next: 0.58
PMF next: {'0': 0.4203, '1': 0.3426, '2': 0.1615, '3': 0.0556, '4': 0.0155, '>=5': 0.0045}

Comparison with a GLM

GLM Poisson in Pyro

Let’s define a vanilla GLM to check the results versus our model. Even thought is a easy model and it could be defined manually, or with simpler libraries, we decided to define it via Pyro.

• \(y \sim \mathrm{Poisson}(\mu)\) same covariates of emissions in the hmm-glm

from pyro.infer import SVI, Trace_ELBO
from pyro.optim import Adam
# Poisson GLM with log link
def glm_poisson_model(X, y=None):
    N, C = X.shape
    beta = pyro.param("betas", torch.zeros(C, device=X.device)) 
    log_mu = (X @ beta.unsqueeze(-1)).squeeze(-1)         # (N,)
    mu = log_mu.exp()
    with pyro.plate("data", N):
        pyro.sample("obs", dist.Poisson(mu), obs=y)

def glm_poisson_guide(X, y=None):
    # Mean-field guide is empty: we use point estimates via pyro.param in the model.
    pass

# Train
def fit_glm_poisson(X, y, steps=3000, lr=1e-2, verbose_every=500, save_path=here("models/glm_poisson_params.pt")):
    X = X.detach()
    y = y.detach().float()
    pyro.clear_param_store()
    svi = SVI(
        lambda X_, y_: glm_poisson_model(X_, y_),
        lambda X_, y_: glm_poisson_guide(X_, y_),
        Adam({"lr": lr}),
        loss=Trace_ELBO()
    )
    loss_hist = []
    for s in range(steps):
        loss = svi.step(X, y)
        if verbose_every and s % verbose_every == 0:
            print(f"step {s:4d}: loss={loss:.3f}")
        loss_hist.append(loss)
    pyro.get_param_store().save(save_path)
    return loss_hist

# Predict and metrics
@torch.no_grad()
def glm_poisson_predict(X):
    X = X.detach()
    beta = pyro.param("betas")
    log_mu = (X @ beta.unsqueeze(-1)).squeeze(-1)
    mu = log_mu.exp()  # expected counts
    return mu

@torch.no_grad()
def glm_poisson_evaluate(X, y):
    """
    Metrics aligned with the HMM printout:
      - pred mean
      - obs mean
      - MSE
      - Accuracy (round)

    If return_all=True, also returns MAE, RMSE, NLL, Brier(y>0).
    """
    X = X.detach()
    y_f = y.detach().float()
    mu = glm_poisson_predict(X)  # (N,)

    # HMM-style metrics
    pred_mean = mu.mean().item()
    obs_mean  = y_f.mean().item()
    mse = torch.mean((mu - y_f) ** 2).item()
    acc_round = torch.mean((torch.round(mu) == y_f).float()).item()
    # acc_round = np.mean(np.round(y_pred_hmm)==y_test)
    mae = torch.mean(torch.abs(mu - y_f)).item()
    rmse = torch.sqrt(torch.mean((mu - y_f) ** 2)).item()
    nll = -torch.mean(dist.Poisson(mu).log_prob(y_f)).item()
    brier = torch.mean(((1.0 - torch.exp(-mu)) - (y_f > 0).float()) ** 2).item()

    out = {
        "pred mean": pred_mean,
        "obs mean": obs_mean,
        "MAE": mae,
        "MSE": mse,
        "RMSE": rmse,
        "Accuracy (round)": acc_round,
        "NLL": nll, 
        "Brier(y>0)": brier
    }

    return out

cov_names_em
xem_train.shape
xem_test[:,-1,:].detach().size()

torch.Size([928, 9])

# y_train: last-year counts, X_train: corresponding covariates
y_train = obs_train[:, -1].float()
x_train = xem_train[:,-1,:]
y_test = obs_test[:, -1].float()
x_test = xem_test[:,-1,:]

loss_hist = fit_glm_poisson(x_train, y_train, steps=20, lr=1e-1, verbose_every=2)
y_pred_glm = glm_poisson_predict(x_test)

step    0: loss=11023.613
step    2: loss=10768.171
step    4: loss=10734.557
step    6: loss=10713.542
step    8: loss=10727.856
step   10: loss=10709.547
step   12: loss=10709.694
step   14: loss=10701.318
step   16: loss=10697.188
step   18: loss=10683.230

pyro.param("betas")

tensor([-0.1311, -0.4747,  0.0392,  0.1969,  0.3996,  0.4512,  0.3716, -0.0153,
         0.0000], requires_grad=True)

Evaluation

Save and load the model

# pyro.get_param_store().load(here("models/glm_poisson_params.pt"))
metrics_glm = glm_poisson_evaluate(x_test, y_test)
print(f"GLM: pred mean={metrics_glm['pred mean']:.2f}  obs mean={metrics_glm['obs mean']:.2f}")
print(f"MAE: {metrics_glm['MAE']:.4f}")
print(f"MSE: {metrics_glm['MSE']:.4f}")
print(f"RMSE: {metrics_glm['RMSE']:.4f}")
print(f"Accuracy (round): {100*metrics_glm['Accuracy (round)']:.2f}%")

GLM: pred mean=0.99  obs mean=0.91
MAE: 0.8473
MSE: 1.0184
RMSE: 1.0092
Accuracy (round): 27.69%

Prediction with HMM

EPS = 1e-30

def softmax_row(x):
    x = x - x.max(axis=-1, keepdims=True)
    e = np.exp(x)
    return e / e.sum(axis=-1, keepdims=True)

def hmm_forward_predict(
    obs_so_far, xpi, xA, A_base, W_pi, W_A, pi_base, beta_em, cov_emission,
    steps_ahead=1,
    pick_one_state=False,
):
    """
    Predicts E[y_{T+steps_ahead}] with covariate-driven transitions and GLM emissions.

    Parameters
    ----------
    obs_so_far : (N, T_obs) array or None
        Observed history (used only for its length; no filtering).
    xpi : (N, C_pi) float
        Initial-state covariates.
    xA : (N, T_total, C_A) float
        Transition covariates for all times (must cover prediction index).
    A_base : (K, K) float, rows simplex
        Base transition matrix.
    W_pi : (K, C_pi) float
        Initial-state slopes.
    W_A : (K, K, C_A) float
        Transition slopes (row-wise).
    pi_base : (K,) float, simplex
        Base initial state.
    beta_em : (K, 1 + C_em) float
        Emission GLM coefficients (intercept + slopes) per state.
    cov_emission : (N, T_total, C_em) float
        Emission covariates at each time.
    steps_ahead : int
        How many steps ahead from T_obs to predict (>=1).
    pick_one_state : boolean
        Pick from last state the most probable or take the entire distribution

    Returns
    -------
    y_expected : (N,) float
        Predicted expected donations at prediction time.
    state_dist : (N, K) float
        Belief on hidden state at prediction time (after propagation).
    """
    N = xpi.shape[0]
    K = beta_em.shape[0]
    T_obs = 0 if (obs_so_far is None) else int(obs_so_far.shape[1])

    # 1) Initial alpha via softmax(log π_base + xπ Wπ^T)
    logits_pi = np.log(pi_base + EPS)[None, :] + xpi @ W_pi.T            # (N,K)
    alpha = softmax_row(logits_pi)                                       # (N,K)

    # 2) Propagation for steps_ahead
    #    For each t in [T_obs, T_obs+steps_ahead-1] build Aprob(n) = softmax_row(log A_base + W_A ⋅ xA[n,t,:])
    logA0 = np.log(A_base + EPS)                                         # (K,K)
    for t in range(T_obs, T_obs + steps_ahead):
        x_t = xA[:, t, :]                                                # (N,C_A)
        # slope logits: tensordot over C_A → (N,K,K)
        slope = np.tensordot(x_t, W_A, axes=([1], [2]))                  # (N,K,K)
        logits = logA0[None, :, :] + slope                               # (N,K,K)
        Aprob = softmax_row(logits)                                      # (N,K,K) row-softmax over axis=-1
        alpha = np.einsum('nk,nkj->nj', alpha, Aprob)                    # (N,K)

    # 3) Emission at prediction time
    t_pred = T_obs + steps_ahead - 1
    x_em = cov_emission[:, t_pred, :]                                    # (N,C_em)
    B  = beta_em[:, :]                                                  # (K,C_em)
    eta = x_em @ B.T                                                # (N,K)
    lam = np.exp(eta)                                                    # (N,K)

    # Expected count under mixture
    if pick_one_state:
        # in questo caso considero solo le emissioni dello stato massimo. Si discosta dall'approccio bayesiano ma aumenta la accuracy e peggiora il MAE,RMSE e MSE
        final_state = np.argmax(alpha, axis=1)      # (N,)
        y_expected = lam[np.arange(N), final_state] # (N,)
    else:
        y_expected = (alpha * lam).sum(axis=1)                               # (N,)

    return y_expected, alpha

beta_em.shape
# xem_test_np.shape

(3, 9)

# Carica parametri
#W_pi, W_A, pi_base, A_base, beta_em = load_hmm_params("hmm_params.pt")

# Converte tensori PyTorch -> NumPy
obs_test_np         = obs_test.detach().cpu().numpy()
xpi_test_np         = xpi_test.detach().cpu().numpy()
xA_test_np          = xA_test.detach().cpu().numpy()
xem_test_np= xem_test.detach().cpu().numpy()

# Predici y_T (one-step ahead) usando osservazioni fino a T-1
y_pred_hmm, state_prob = hmm_forward_predict(
    obs_so_far      = obs_test_np[:, :-1],     # up to T-1
    xpi             = xpi_test_np,
    xA              = xA_test_np,
    A_base          = A_base,
    W_pi            = W_pi,
    W_A             = W_A,
    pi_base         = pi_base,
    beta_em         = beta_em,
    cov_emission    = xem_test_np,    # (N_test, T, C_em)
    steps_ahead     = 1,
    pick_one_state  = False,
)
# take just the most  probable state
y_pred_hmm_one_state, _ = hmm_forward_predict(
    obs_so_far      = obs_test_np[:, :-1],     # up to T-1
    xpi             = xpi_test_np,
    xA              = xA_test_np,
    A_base          = A_base,
    W_pi            = W_pi,
    W_A             = W_A,
    pi_base         = pi_base,
    beta_em         = beta_em,
    cov_emission    = xem_test_np,    # (N_test, T, C_em)
    steps_ahead     = 1,
    pick_one_state  = True,
)

y_test = obs_test_np[:, -1]
print(f"HMM(full): pred mean={y_pred_hmm.mean():.2f}  obs mean={y_test.mean():.2f}")
print(f"MAE: {np.mean(np.abs(y_pred_hmm - y_test)):.4f}")
print(f"MSE: {np.mean((y_pred_hmm - y_test)**2):.4f}")
print(f"RMSE: {np.sqrt(np.mean((y_pred_hmm - y_test) ** 2)):.4f}")
print(f"Accuracy (round): {100*np.mean(np.round(y_pred_hmm)==y_test):.2f}%")
print(f"Accuracy one state (round): {100*np.mean(np.round(y_pred_hmm_one_state)==y_test):.2f}%")

HMM(full): pred mean=0.55  obs mean=0.91
MAE: 0.8511
MSE: 1.2480
RMSE: 1.1171
Accuracy (round): 39.98%
Accuracy one state (round): 42.46%

def _to_numpy1d(x):
    if isinstance(x, torch.Tensor):
        x = x.detach().cpu().numpy()
    return np.asarray(x, dtype=float).ravel()

def build_hmm_metrics(y_pred_hmm, y_test):
    y_pred = _to_numpy1d(y_pred_hmm)
    y_true = _to_numpy1d(y_test)
    return {
        "pred mean": float(np.mean(y_pred)),
        "obs mean":  float(np.mean(y_true)),
        "MAE":       float(np.mean(np.abs(y_pred - y_true))),
        "MSE":       float(np.mean((y_pred - y_true) ** 2)),
        "RMSE":       float(np.sqrt(np.mean((y_pred - y_true) ** 2))),
        "Accuracy (round)": float(np.mean(np.round(y_pred) == y_true)),
    }

def pct_rel_diff(a, b, eps=1e-12):
    return 100.0 * (a - b) / (abs(b) + eps)

def print_comparison_table(metrics_glm, metrics_hmm):
    print(f"{'Metric':<20} {'GLM':>14} {'HMM':>14} {'Abs diff':>14} {'Rel diff %':>12}")
    print("-" * 76)
    order = ["pred mean", "obs mean", "MAE", "MSE", "RMSE", "Accuracy (round)"]
    for key in order:
        g = metrics_glm[key]
        h = metrics_hmm[key]
        if key == "Accuracy (round)":
            g_disp = 100.0 * g
            h_disp = 100.0 * h
            abs_disp = 100.0 * (g - h)          # punti percentuali
            rel_pct = pct_rel_diff(g, h)
            print(f"{key:<20} {g_disp:14.2f}% {h_disp:14.2f}% {abs_disp:14.2f}pp {rel_pct:11.2f}%")
        elif key == "MSE":
            abs_diff = g - h
            rel_pct = pct_rel_diff(g, h)
            print(f"{key:<20} {g:14.2f} {h:14.2f} {abs_diff:14.2f} {rel_pct:11.2f}%")
        else:
            abs_diff = g - h
            rel_pct = pct_rel_diff(g, h)
            print(f"{key:<20} {g:14.2f} {h:14.2f} {abs_diff:14.2f} {rel_pct:11.2f}%")

metrics_hmm = build_hmm_metrics(y_pred_hmm, y_test)

print_comparison_table(metrics_glm, metrics_hmm)

Metric                          GLM            HMM       Abs diff   Rel diff %
----------------------------------------------------------------------------
pred mean                      0.99           0.56           0.43       77.67%
obs mean                       0.91           0.91           0.00        0.00%
MAE                            0.85           0.85          -0.00       -0.40%
MSE                            1.02           1.24          -0.23      -18.15%
RMSE                           1.01           1.12          -0.11       -9.53%
Accuracy (round)              27.69%          40.52%         -12.82pp      -31.65%

def plot_accuracy(glm_acc, hmm_acc):
    """
    Plotta le accuracy di GLM e HMM.
    
    Args:
        glm_acc (float): Accuracy del GLM (in percento o frazione).
        hmm_acc (float): Accuracy dell'HMM (in percento o frazione).
    """
    # Se i valori sono frazioni (0-1), li porto in percento
    if glm_acc <= 1 and hmm_acc <= 1:
        glm_acc *= 100
        hmm_acc *= 100
    
    methods = ["GLM", "HMM"]
    values = [glm_acc, hmm_acc]

    plt.figure(figsize=(5,4))
    bars = plt.bar(methods, values, color=hmm_pl.palette, edgecolor="black")
    
    # Aggiungo etichette sopra le barre
    for bar, val in zip(bars, values):
        plt.text(bar.get_x() + bar.get_width()/2, val + 0.5, f"{val:.2f}%", 
                 ha="center", va="bottom", fontsize=10)
    
    plt.ylabel("Accuracy (%)")
    plt.title("Confronto Accuracy: GLM vs HMM")
    plt.ylim(0, max(values) + 10)
    plt.show()

import json
metrics_to_save = {
    "Accuracy_glm": metrics_glm["Accuracy (round)"],
    "Accuracy_hmm": metrics_hmm["Accuracy (round)"]
}
with open(here("Python/metrics.json"), "w") as f:
    json.dump(metrics_to_save, f)

plot_accuracy(metrics_glm["Accuracy (round)"], metrics_hmm["Accuracy (round)"]) 
# plot_accuracy(28.23, 40.73)  # esempio con valori fittizi   

df_pred = pd.DataFrame({
    "y_pred_hmm_multi_state": y_pred_hmm,
    "y_pred_hmm_one_state": y_pred_hmm_one_state,
    "y_test": y_test,
    # "y_test": y_test.detach().cpu().numpy().ravel(),
    "y_pred_glm": torch.round(y_pred_glm).int().detach().cpu().numpy().ravel(),
})
df_pred["error_hmm_ms"] = df_pred["y_pred_hmm_multi_state"].round() - df_pred["y_test"]
df_pred["error_hmm_os"] = df_pred["y_pred_hmm_one_state"].round() - df_pred["y_test"]
df_pred["error_glm"] = df_pred["y_pred_glm"].round() - df_pred["y_test"]
df_pred["error_glm_rounded"] = df_pred["error_glm"].astype(int)
df_pred["error_hmm_ms_rounded"] = df_pred["error_hmm_ms"].astype(int)
df_pred["error_hmm_os_rounded"] = df_pred["error_hmm_os"].astype(int)

df_pred.to_csv(here("models/metrics_df.csv"), index=False)

plt.figure(figsize=(8, 5))
plt.boxplot([df_pred["error_hmm_os"],df_pred["error_hmm_ms"], df_pred["error_glm"]], labels=["HMM one-states errori", "HMM multi-states errori", "GLM errori"])
plt.ylabel("Errore (Predizione - Reale)")
plt.title("Distribuzione degli errori predittivi")
plt.grid(True, linestyle="--", alpha=0.5)
plt.show()

<positron-console-cell-67>:2: MatplotlibDeprecationWarning: The 'labels' parameter of boxplot() has been renamed 'tick_labels' since Matplotlib 3.9; support for the old name will be dropped in 3.11.

def plot_error_distribution(errors, title, ax):
    full_range = pd.Series(range(-4,5), name="error")
    freq = errors.value_counts(normalize=True).sort_index() * 100
    freq_df = freq.reset_index()
    freq_df.columns = ["error", "percent"]
    freq_df = full_range.to_frame().merge(freq_df, on="error", how="left").fillna(0)
    pivot_df = freq_df.pivot_table(index="error", values="percent")
    sns.heatmap(
        pivot_df.T,
        annot=True,
        fmt=".2f",
        cmap=hmm_pl.COEFF_CMAP,
        cbar_kws={'label': 'Percentuale (%)'} if title=="GLM" else None,
        linewidths=0.5,
        linecolor='gray',
        ax=ax,
        vmin=0, vmax=freq_df["percent"].max()  # uniform color scale
    )
    ax.set_xlabel("Errore arrotondato")
    ax.set_ylabel("")
    ax.set_yticks([])
    ax.set_title(f"Distribuzione percentuale errori {title}")
    ax.set_xticklabels(range(-4,5))

fig, axes = plt.subplots(3,1, figsize=(10,6), sharex=True)
plot_error_distribution(df_pred["error_glm_rounded"], "GLM", axes[0])
plot_error_distribution(df_pred["error_hmm_os_rounded"], "HMM-GLM one-state", axes[1])
plot_error_distribution(df_pred["error_hmm_ms_rounded"], "HMM-GLM multi-states", axes[2])

plt.tight_layout()
plt.show()

Confusion Matrix

# unique, counts = np.unique(y_pred_binary, return_counts=True)
# unique, counts = np.unique(y_true_binary, return_counts=True)
# for value, count in zip(unique, counts):
#     print(f"Valore: {value}, Frequenza: {count}")
    
# y_true_binary

Valore: 0, Frequenza: 426
Valore: 1, Frequenza: 502

def matthews_corrcoef(tp, tn, fp, fn):
    numerator = (tp * tn) - (fp * fn)
    denominator = ((tp + fp) * (tp + fn) * (tn + fp) * (tn + fn)) ** 0.5
    if denominator == 0:
        return 0
    return numerator / denominator

# y_pred_binary = np.where(y_pred_hmm.round() > 0, 1, 0)
y_pred_binary = np.where(y_pred_hmm > 0.23, 1, 0)
y_true_binary = np.where(y_test > 0, 1, 0)

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_true_binary, y_pred_binary)
print(cm)  # [[TN, FP], [FN, TP]]

tn, fp, fn, tp = cm.ravel()

mcc = matthews_corrcoef(tp, tn, fp, fn)
print("Matthews correlation coefficient:", f"{mcc:2.3}")

[[167 259]
 [131 371]]
Matthews correlation coefficient: 0.14

The plot show how good is the model in the prediction if a donor next year is going to donate or less. The model is not performing very well in this scenario

from sklearn.metrics import roc_curve, roc_auc_score

y_true_binary = np.where(y_test > 0, 1, 0)

fpr, tpr, thresholds = roc_curve(y_true_binary, y_pred_hmm)
auc = roc_auc_score(y_true_binary, y_pred_hmm)

# Disegna la curva
plt.figure(figsize=(7,7))
plt.plot(fpr, tpr, color="purple", label=f"AUC = {auc:0.3f}")
plt.plot([0,1], [0,1], color="grey", linestyle="--")
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("ROC Curve")
plt.legend()
plt.show()

Number of latent states

import hmm_glm_prediction 

# functioon for building model and guide with covariates and K states 
def make_hmm_model_and_guide_cov(K):
    @config_enumerate
    def model(obs, x_pi, x_A, x_em):
        # forza obs a torch.Tensor
        obs = torch.as_tensor(obs)
        N, T = obs.shape
        C_pi = x_pi.shape[1]
        C_A  = x_A.shape[2]
        C_em = x_em.shape[2]

        # Priors
        alpha_pi = 0.5 * torch.ones(K)        # <1 → più “spiky”
        alpha_A  = torch.full((K, K), 0.5)
        alpha_A.fill_diagonal_(6.0)           # forte massa in diagonale
        
        pi_base = pyro.sample("pi_base", dist.Dirichlet(alpha_pi))             # [K]
        A_base  = pyro.sample("A_base",  dist.Dirichlet(alpha_A).to_event(1))  # [K,K]
        
        log_pi_base = pi_base.log()
        log_A_base  = A_base.log()

        # Parametri globali
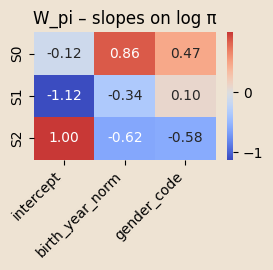
        W_pi  = pyro.param("W_pi", 0.01 * torch.randn(K, C_pi))
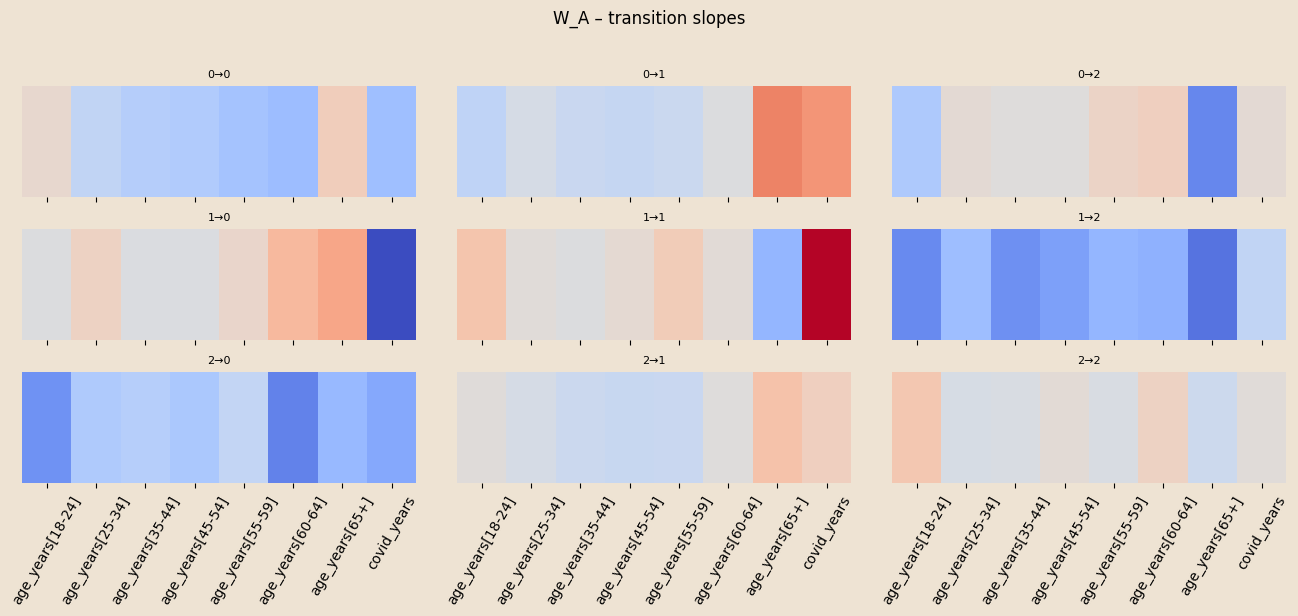
        W_A   = pyro.param("W_A",  0.01 * torch.randn(K, K, C_A))
        beta_em = pyro.param("beta_em", 0.01 * torch.randn(K, C_em))
        
        with pyro.plate("seqs", N):
            # stato iniziale
            logits0 = log_pi_base + (x_pi @ W_pi.T)
            z_prev = pyro.sample("z_0", dist.Categorical(logits=logits0),
                                infer={"enumerate": "parallel"})
            
            log_mu_0 = (x_em[:, 0, :] * beta_em[z_prev, :]).sum(-1)
            pyro.sample("y_0", dist.Poisson(log_mu_0.exp()), obs=obs[:, 0])

            # transizioni
            for t in range(1, T):
                x_t = x_A[:, t, :]
                
                logitsT = (log_A_base[z_prev] + (W_A[z_prev] * x_t[:, None, :]).sum(-1))
                z_t = pyro.sample(f"z_{t}", dist.Categorical(logits=logitsT),
                                infer={"enumerate": "parallel"})
                
                log_mu_t = (x_em[:, t, :] * beta_em[z_t, :]).sum(-1)
                pyro.sample(f"y_{t}", dist.Poisson(log_mu_t.exp()), obs=obs[:, t])
                
                z_prev = z_t
        
      
    def guide(obs, x_pi, x_A, x_em):
        # forza obs a torch.Tensor
        obs = torch.as_tensor(obs)
        # Parametri MAP per pi e A
        pi_q = pyro.param("pi_base_map",
                        torch.ones(K) / K,
                        constraint=dist.constraints.simplex)

        A_init = torch.eye(K) * (K - 1.) + 1.
        A_init = A_init / A_init.sum(-1, keepdim=True)
        A_q = pyro.param("A_base_map",
                        A_init,
                        constraint=dist.constraints.simplex)

        pyro.sample("pi_base", dist.Delta(pi_q).to_event(1))
        pyro.sample("A_base",  dist.Delta(A_q).to_event(2))

    
    #num_params = K * x_pi.shape[1] + K * K * x_A.shape[2] + K * (x_em.shape[2] + 1) + K + K*K


    return model, guide

# Reads the variational parameters from the ParamStore and returns point estimates.
@torch.no_grad()
def extract_posterior_point_estimates_cov():
    
    store = pyro.get_param_store()

    def softmax_row(v):
        e = np.exp(v - np.max(v, axis=-1, keepdims=True))
        return e / e.sum(axis=-1, keepdims=True)

    # 1) Extract learned parameters
    pi_base = pyro.param("pi_base_map").detach().cpu().numpy()      # (K,) simplex
    A_base  = pyro.param("A_base_map").detach().cpu().numpy()       # (K, K) rows on simplex
    W_pi    = pyro.param("W_pi").detach().cpu().numpy()             # (K, C_pi)
    W_A     = pyro.param("W_A").detach().cpu().numpy()              # (K, K, C_A)
    beta_em = pyro.param("beta_em").detach().cpu().numpy()          # (K, 1 + C_em) if intercept first


    # 2) Covariate means
    x_mean_pi = cov_init_torch.mean(dim=0).detach().cpu().numpy()        # (C_pi,)
    x_mean_A  = cov_tran_torch.mean(dim=(0, 1)).detach().cpu().numpy()   # (C_A,)
    x_mean_em = cov_emiss_torch.mean(dim=(0,1)).detach().cpu().numpy()   # (C_em,)


    # 3) Mean initial probs, transitions and rates under average covariates
    logits_pi = np.log(pi_base + 1e-30) + W_pi @ x_mean_pi
    pi_mean   = softmax_row(logits_pi[None, :]).ravel()

    K = pi_mean.shape[0]
    A_mean = np.zeros((K, K))
    for k in range(K):
        logits_row = np.log(A_base[k] + 1e-30) + (W_A[k] @ x_mean_A)
        A_mean[k] = softmax_row(logits_row[None, :]).ravel()
   
    rates_mean = np.zeros(K)
    for k in range(K):
        log_mu = np.dot(x_mean_em, beta_em[k, :])
        rates_mean[k] = np.exp(log_mu)

    return pi_mean, A_mean, rates_mean

# Uses the learned parameters from the ParamStore to make predictions on test data, compute MSE and Accuracy, and display a plot."
def evaluate_hmm_glm_prediction(obs_test, xpi_test, xA_test, xem_test):
    
    store = pyro.get_param_store()

    def softmax_row(v):
        e = np.exp(v - np.max(v, axis=-1, keepdims=True))
        return e / e.sum(axis=-1, keepdims=True)

    # 1) Extract learned parameters
    pi_base = pyro.param("pi_base_map").detach().cpu().numpy()      # (K,)
    A_base  = pyro.param("A_base_map").detach().cpu().numpy()       # (K, K)
    W_pi    = pyro.param("W_pi").detach().cpu().numpy()             # (K, C_pi)
    W_A     = pyro.param("W_A").detach().cpu().numpy()              # (K, K, C_A)
    beta_em = pyro.param("beta_em").detach().cpu().numpy()          # (K, 1 + C_em)

    # 2) Convert test data to NumPy
    obs_test_np          = obs_test.detach().cpu().numpy()
    xpi_test_np          = xpi_test.detach().cpu().numpy()
    xA_test_np           = xA_test.detach().cpu().numpy()
    xem_test_np = xem_test.detach().cpu().numpy()

    # 3) One-step ahead prediction
    y_pred_hmm, state_prob = hmm_forward_predict(
        obs_so_far=obs_test_np[:, :-1],
        xpi=xpi_test_np,
        xA=xA_test_np,
        A_base=A_base,
        W_pi=W_pi,
        W_A=W_A,
        pi_base=pi_base,
        beta_em=beta_em,
        cov_emission=xem_test_np,
        steps_ahead=1
    )

    # 4) True values
    y_test = obs_test_np[:, -1]

    # 5) Compute metrics
    mse = np.mean((y_pred_hmm - y_test)**2)
    acc = 100*np.mean(np.round(y_pred_hmm) == y_test)

    print(f"HMM(full): pred mean={y_pred_hmm.mean():.2f}  obs mean={y_test.mean():.2f}")
    print(f"MSE: {mse:.4f}")

    return y_pred_hmm, y_test, mse, acc

# def log_softmax_logits(logits, dim=-1):
#     return logits - torch.logsumexp(logits, dim=dim, keepdim=True)

# Computes the forward algorithm log-likelihood for a covariate-dependent HMM with Poisson emissions using the parameters stored in the Pyro ParamStore.
@torch.no_grad()
def forward_loglik_cov(obs, x_pi, x_A, x_em):
    device = obs.device
    ps = pyro.get_param_store()
    pi_base = ps["pi_base_map"].to(device)
    A_base  = ps["A_base_map"].to(device)
    W_pi    = ps["W_pi"].to(device)
    W_A     = ps["W_A"].to(device)
    beta_em = ps["beta_em"].to(device)

    N, T = obs.shape
    K = pi_base.shape[0]
    B  = beta_em[:, :]
    log_mu = torch.einsum("ntc,kc->ntk", x_em.to(device), B)
    emis_log = dist.Poisson(rate=log_mu.exp()).log_prob(obs.unsqueeze(-1))  # (N,T,K)

    log_pi = log_softmax_logits(pi_base.log() + x_pi @ W_pi.T, dim=1)       # (N,K)
    log_alpha = log_pi + emis_log[:, 0]

    log_A0 = A_base.log()
    for t in range(1, T):
        x_t = x_A[:, t, :]
        logits = log_A0.unsqueeze(0) + (W_A.unsqueeze(0) * x_t[:, None, None, :]).sum(-1)
        log_A = log_softmax_logits(logits, dim=2)
        log_alpha = torch.logsumexp(log_alpha.unsqueeze(2) + log_A, dim=1) + emis_log[:, t]
    return torch.logsumexp(log_alpha, dim=1)  # (N,)

# Evaluate HMM-GLM models with different numbers of latent states, evaluates them using log-evidence and prediction accuracy
def train_and_evaluate_cov(obs_torch, x_pi, x_A, x_em, K_list, n_steps=500, lr=1e-5):

    log_evidences = []
    final_elbos = []        # salvo gli ELBO finali
    accuracies = []         # salvo le accuracy

    for K in K_list:
        print(f"\n=== Training HMM with K={K} states ===")
        
        # crea modello e guida
        model, guide = make_hmm_model_and_guide_cov(K)

        # resetta ParamStore
        pyro.clear_param_store()

        svi = SVI(model, guide,
                  Adam({"lr": lr}),
                  loss=TraceEnum_ELBO(max_plate_nesting=1))

        losses = []
        for step in range(n_steps):
            loss = svi.step(obs_torch, x_pi, x_A, x_em)
            losses.append(loss)
            if step % 50 == 0:
                print(f"K={K} | step {step:4d}  ELBO = {loss:,.0f}")
        
        # ELBO finale
        final_elbo_val = -losses[-1]
        final_elbos.append(final_elbo_val)

        # 🔹 calcolo metriche di prediction (inclusa accuracy)
        _, _, mse, acc = evaluate_hmm_glm_prediction(obs_torch, x_pi, x_A, x_em)
        accuracies.append(acc)

        # calcola log-likelihood / evidenza
        log_evidence_val = forward_loglik_cov(obs_torch, x_pi, x_A, x_em).sum()
        log_evidences.append(log_evidence_val)
        print(f"Log-evidence K={K}: {log_evidence_val:.2f}")
        print(f"Accuracy K={K}: {acc:.2f}%")

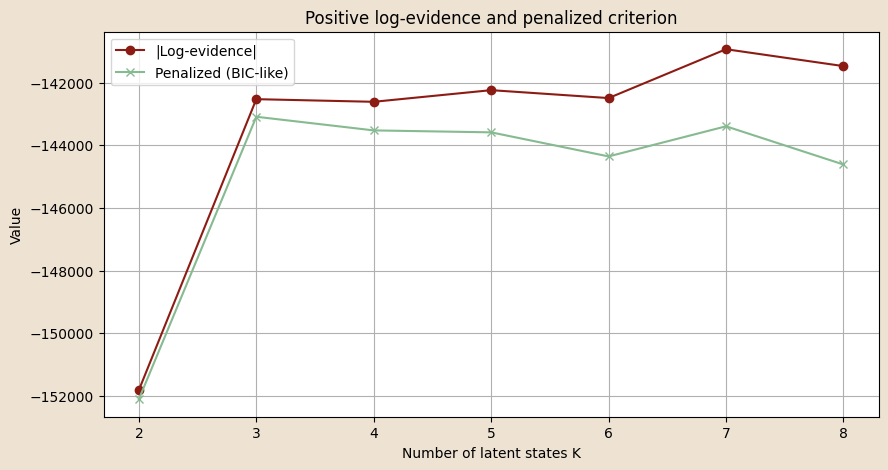
    # 🔹 Plot evidenze e ELBO
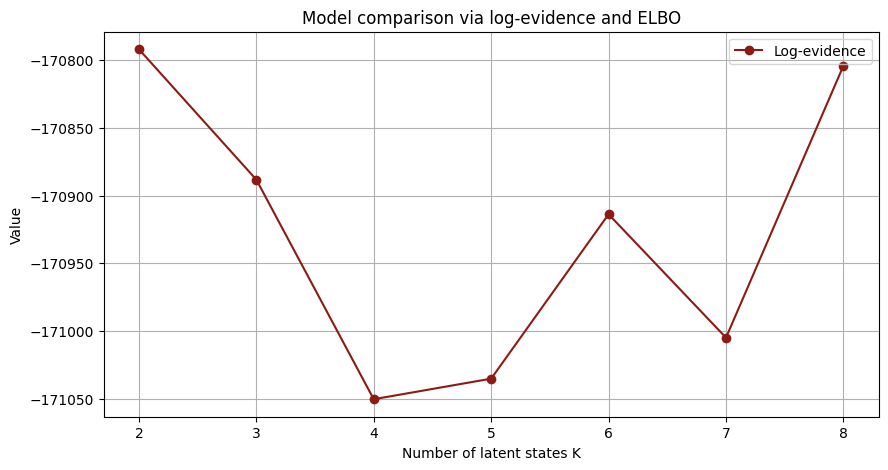
    plt.figure(figsize=(10,5))
    plt.plot(K_list, log_evidences, marker='o', label="Log-evidence")
    #plt.plot(K_list, final_elbos, marker='x', label="Final ELBO")
    plt.xlabel("Number of latent states K")
    plt.ylabel("Value")
    plt.title("Model comparison via log-evidence and ELBO")
    plt.legend()
    plt.grid(True)
    plt.show()

    # 🔹 Plot accuracy come istogramma
    plt.figure(figsize=(8,5))
    plt.bar([str(K) for K in K_list], accuracies, color="skyblue")
    plt.xlabel("Number of latent states K")
    plt.ylabel("Accuracy (%)")
    plt.title("Prediction Accuracy by Model (HMM-GLM)")
    plt.grid(axis="y", linestyle="--", alpha=0.7)

    # settaggio asse y
    y_min = 30
    y_max = max(accuracies) + 2  # così lasci un po’ di margine sopra
    plt.ylim(y_min, y_max)
    plt.yticks(np.arange(y_min, y_max+1, 2))  # tick ogni 2

    plt.show()
    return K_list, log_evidences, final_elbos, accuracies 

K_list = range(2, 9)
K_list, log_evidences, final_elbos, accuracies = train_and_evaluate_cov(obs_torch, cov_init_torch, cov_tran_torch, cov_emiss_torch, K_list, n_steps=51, lr=2e-3)

=== Training HMM with K=2 states ===
K=2 | step    0  ELBO = 177,307
K=2 | step   50  ELBO = 170,892
HMM(full): pred mean=0.89  obs mean=0.97
MSE: 1.0507
Log-evidence K=2: -170791.88
Accuracy K=2: 28.79%

=== Training HMM with K=3 states ===
K=3 | step    0  ELBO = 177,558
K=3 | step   50  ELBO = 170,989
HMM(full): pred mean=0.90  obs mean=0.97
MSE: 1.0491
Log-evidence K=3: -170888.22
Accuracy K=3: 28.79%

=== Training HMM with K=4 states ===
K=4 | step    0  ELBO = 177,724
K=4 | step   50  ELBO = 171,146
HMM(full): pred mean=0.90  obs mean=0.97
MSE: 1.0515
Log-evidence K=4: -171050.48
Accuracy K=4: 28.79%

=== Training HMM with K=5 states ===
K=5 | step    0  ELBO = 177,753
K=5 | step   50  ELBO = 171,121
HMM(full): pred mean=0.89  obs mean=0.97
MSE: 1.0526
Log-evidence K=5: -171035.30
Accuracy K=5: 28.79%

=== Training HMM with K=6 states ===
K=6 | step    0  ELBO = 177,576
K=6 | step   50  ELBO = 170,984
HMM(full): pred mean=0.90  obs mean=0.97
MSE: 1.0504
Log-evidence K=6: -170913.81
Accuracy K=6: 28.79%

=== Training HMM with K=7 states ===
K=7 | step    0  ELBO = 177,680
K=7 | step   50  ELBO = 171,054
HMM(full): pred mean=0.90  obs mean=0.97
MSE: 1.0499
Log-evidence K=7: -171005.00
Accuracy K=7: 28.79%

=== Training HMM with K=8 states ===
K=8 | step    0  ELBO = 177,363
K=8 | step   50  ELBO = 170,828
HMM(full): pred mean=0.89  obs mean=0.97
MSE: 1.0520
Log-evidence K=8: -170804.06
Accuracy K=8: 28.79%

log_evidences

[tensor(-170791.8750),
 tensor(-170888.2188),
 tensor(-171050.4844),
 tensor(-171035.2969),
 tensor(-170913.8125),
 tensor(-171005.),
 tensor(-170804.0625)]

C_pi = cov_init_torch.shape[1]
C_A  = cov_tran_torch.shape[2]
C_em = cov_emiss_torch.shape[2]


K_list = list(range(2, 9))
log_evidences = np.array([
   -151813.3281,
 -142526.,
 -142610.1406,
 -142238.3438,
 -142491.0469,
 -140931.5000,
 -141470.5000
])

# rendiamo valori positivi
#log_evidences_pos = np.abs(log_evidences)

# calcoliamo num_params per ciascun K
num_params_list = []
for K in K_list:
    num_params = K * C_pi + K * K * C_A + K * (C_em + 1) + K + K*K
    num_params_list.append(num_params)
num_params_list = np.array(num_params_list)

# numero di sequenze
N = 9236

# criterio penalizzato stile BIC
penalized = log_evidences - 0.5 * num_params_list * np.log(N)

# plot
plt.figure(figsize=(10, 5))
plt.plot(K_list, log_evidences, marker='o', label='Log-evidence')
plt.plot(K_list, penalized, marker='x', label='Penalized (BIC-like)')
plt.xlabel("Number of latent states K")
plt.ylabel("Value")
plt.title("Positive log-evidence and penalized criterion")
plt.grid(True)
plt.legend()
plt.savefig(here("thesis/img/hmm/bic_plot.png"), dpi=300, bbox_inches="tight", transparent=True)
plt.show()